The "Sum of Squares Total" in ANOVA
Many of the computer implementations of ANOVA, including the one
in Excel, print out two values that are not used in the later
steps of ANOVA: the sum of the SSE (the sum of the squared
deviations within samples from the sample averages) and the SSG
(the sum of the squared deviations of the sample averages from
the overall average, weighted by the size of the samples), and the
sum of the DFE and the DFG. The first of these is
often denoted SST and called the "total squared deviation
(from the average)", because it is also equal to the sum of the squared
deviations of all the data values from the grand average. And the
second, denoted DFT, is called the total degrees of freedom.
It is easy to see that
DFT = DFE + DFG =
(N - I) + (I - 1) = N - 1,
and this
is a reasonable quantity to call the "total degrees of freedom". But
it is not so obvious that the two ways of interpreting SST,
on the one hand as the sum of SSE and SSG, and
on the other hand as the sum
of the squares of the differences of the data values from the overall
average, give the same value. It implies the following equation (which
I must render as a graphic because of the limitations of HTML):
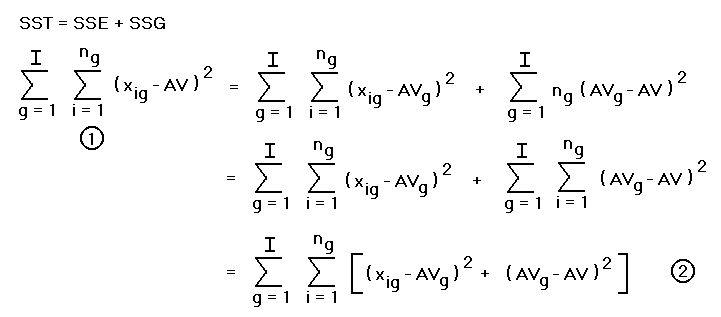
At first glance, it looks reasonable that the two end expressions
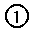 and
and 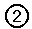 are equal. But in
general, it is not true that
are equal. But in
general, it is not true that
(A - B)2 + (B - C)2
= (A - C)2
Because of the squaring, there are several "middle
terms" in these expressions. In this case, do
they really "cancel out", to make the two interpretations of SST
really equal? To see why it works here, we note first that the definitions
of AVg and AV give us some substitutions to use:
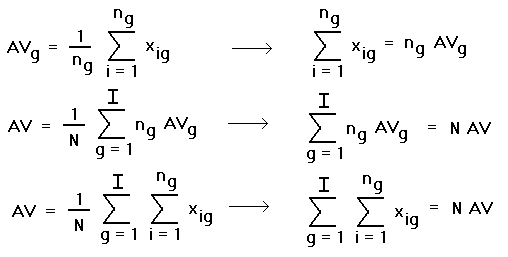
Using these and some familiar facts about
summations, starting with
the more complicated expression  , we have:
, we have:
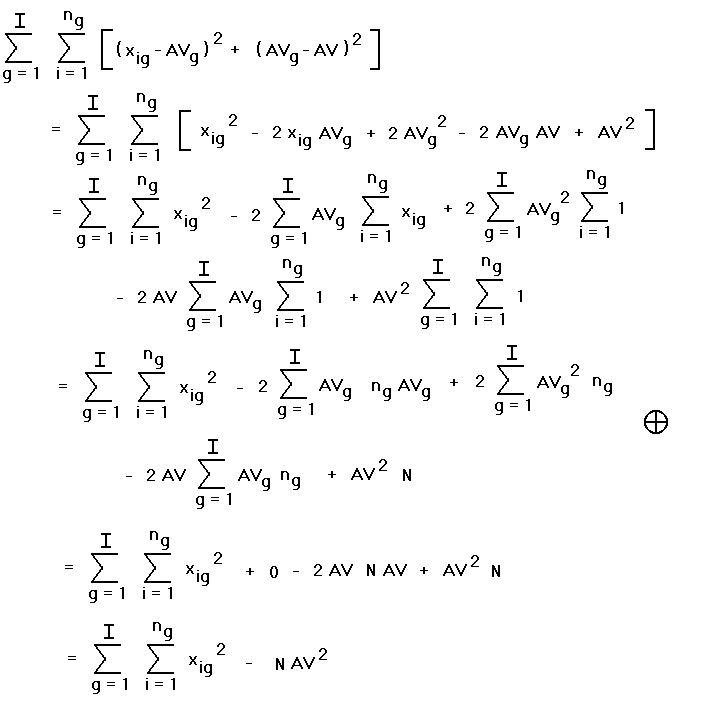
where the second and third terms in the expression
labelled  add to zero. In a similar way,
but working on the expression
add to zero. In a similar way,
but working on the expression  , we have:
, we have:
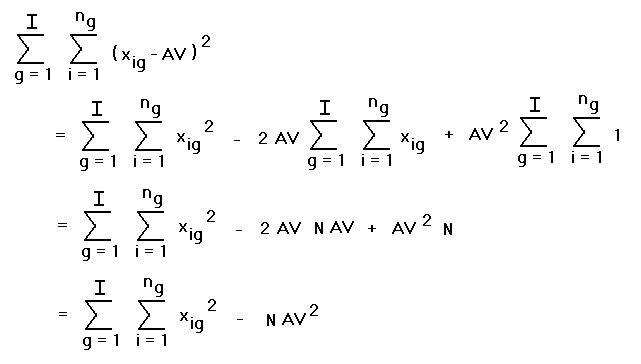
This is the same expression as we got from 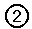 , so
they are indeed equal.
, so
they are indeed equal.
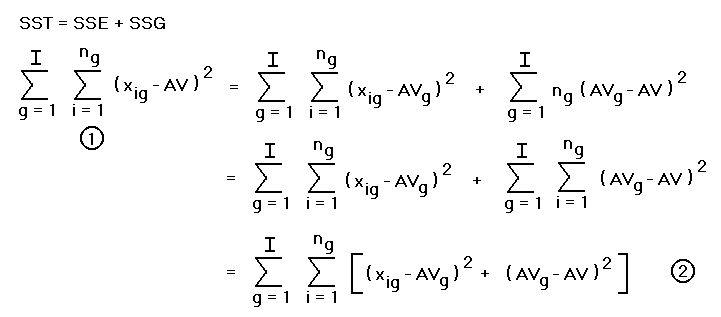
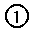 and
and  are equal. But in
general, it is not true that
are equal. But in
general, it is not true that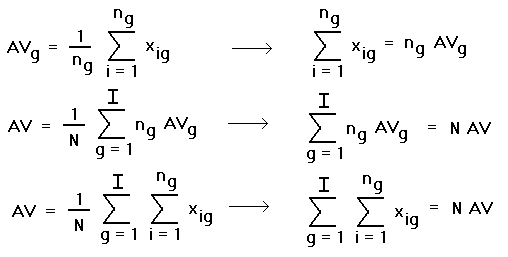
 , we have:
, we have: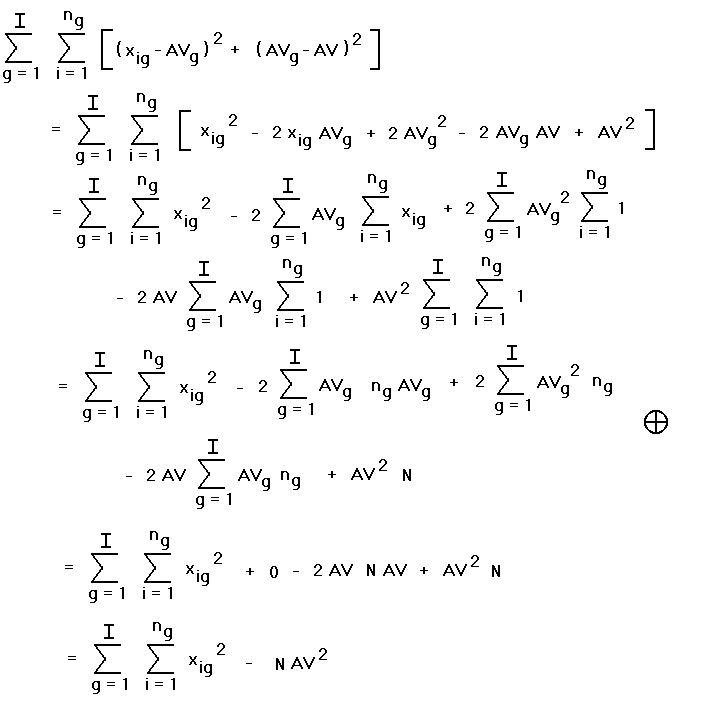
 add to zero. In a similar way,
but working on the expression
add to zero. In a similar way,
but working on the expression  , we have:
, we have: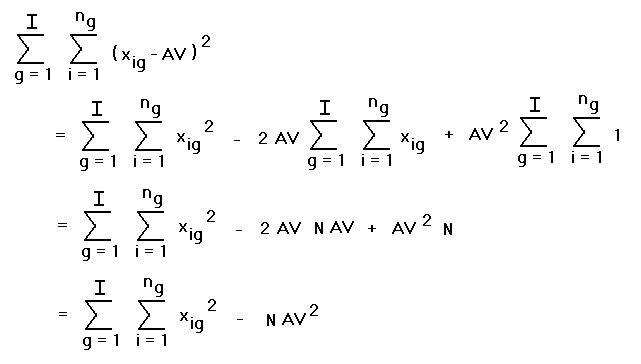
 , so
they are indeed equal.
, so
they are indeed equal.