The Tschirnhausen cubic

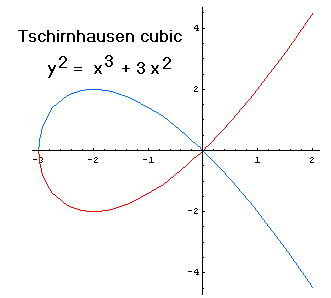
As an example of implicit differentiation, we study the Tschirnhausen cubic.

Since each value of x in the interval x > -3 except x = 0 corresponds two different y-values, the cubic does not determine y as a function of x. The colors in the drawing are meant to suggest one way in which we could divide the cubic into two parts, each of which determines y as a function of x in a different way. But this way of dividing the cubic is not the only possible one; to draw this cubic, I instructed my computer algebra to draw the graphs of the two functions shown here:

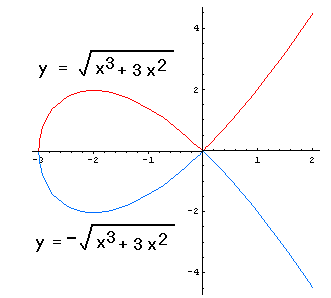
Unlike the two functions in the first picture, these two functions are not differentiable at 0; but they have simple expressions in terms of familiar functions. However the cubic is divided, though, if we focus on a sufficiently small part of the curve, except (-3,0) and (0,0), y appears as a differentiable function of x. In this sense, we say that the equation of the cubic determines y "implicitly" as a function of x (as opposed to an "explicit" definition of y as a function of x, i.e., y = an expression in terms of x only). Suppose we want to find the derivative dy/dx of the function at one of these many "good" points. For this cubic, since it is possible to express the functions explicitly (as written on the graph), we need not use implicit differentiation. But for many curves explicit solutions are not available, so let us try something else. Granting that y is (locally) a function of x, both sides of the defining equation y²=x³+3x² are functions of x, indeed, the same function of x because they are equal. So their derivatives are equal also. Now, although we are avoiding the explicit expression of y in terms of x, we can still use the Chain Rule to write an expression for the derivative with respect to x of the left side of the equation, which must equal the derivative of the right side:

In computing the derivative of the left side, when the Chain Rule demanded that we write the derivative of y with respect to x, we could only write dy/dx, since we do not know y explicitly as a function of x. But we now have an equation in which the very quantity we wanted, dy/dx appears, and in fact it is easy to solve the equation for it -- though the equation may be otherwise complicated, it is linear in dy/dx. Solving for dy/dx gives an expression for the derivative, in terms of both x and y:

It should not be surprising that both variables are needed, because the point on the curve is not uniquely determined by x alone. For example, the tangents at the two points with x-coordinate 1 on this cubic have different slopes:

• At (1,2), we have dy/dx = (3(1)²+6(1))/(2(2)) = 9/4, and
• At (1,-2), we have dy/dx = (3(1)²+6(1))/(2(-2)) = -9/4.

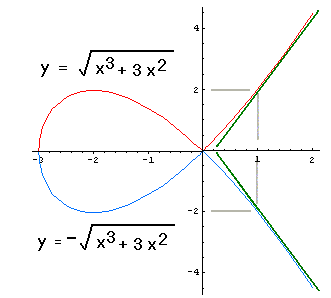
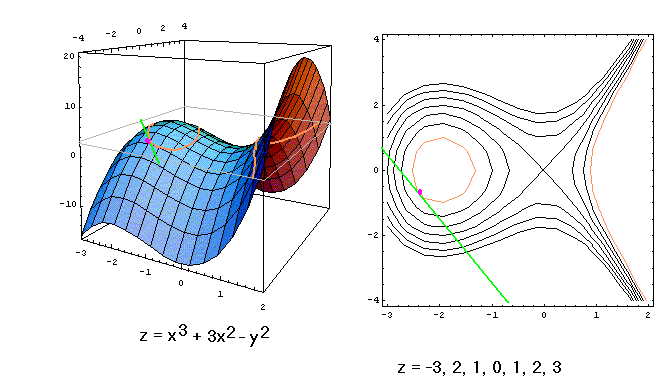
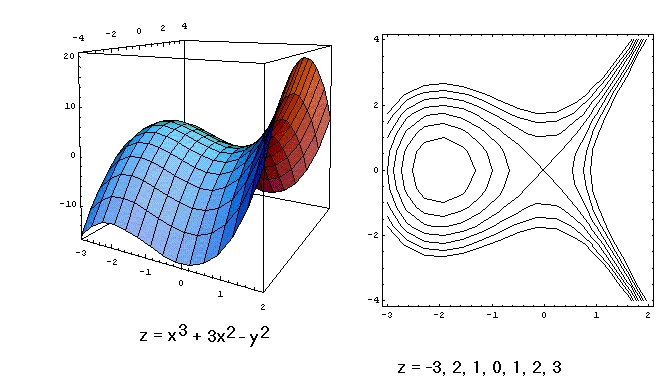
Picking values for z just amounts to slicing this graph with horizontal planes, forming "contours" of the surface. The plane z=0 gives the present cubic; others, for z=-3,-2,-1,1,2,3, have no crossing points (called nodes, as at (0,0) in the original cubic), though for some the graph is disconnected (when the slicing plane is above the origin but not above the "dome" that has high point at (-2,0,4)):

At any point on any one of these curves, we can use the formula

to find the slope of the tangent line. It amounts to finding the slope of a horizontal line tangent to the surface at some point -- the slope being computed in the horizontal xy-plane that cuts the surface at that point.