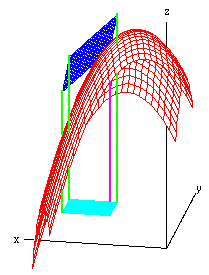
In the graph to the right, the y-axis is aimed roughly over
the viewer's right ear. The plane of the dark blue parallelogram is
tangent to the red surface at a point on the back side of the
surface, the invisible corner of the parallelogram. The parallelogram
is above the light blue rectangle in the xy-plane, with the
lines through the corners of both -- the purple line goes to the
point of tangency.
- red surface: graph of z = f(x,y)
- dark blue: tangent plane to z = f(x,y) at (a,b,f(a,b))
- light blue: rectangle in xy-plane with one corner (a,b,0),
with edges of lengths dx and dy.
- purple line segment from (a,b,0) to (a,b,f(a,b))
- green line segments from (a+dx,b,0) to
(a+dx,b,f(a+dx,b)), from (a,b+dy,0) to
(a,b+dy,f(a,b+dy)), and from (a+dx,b+dy,0) to
(a+dx,b+dy,f(a+dx,b+dy)).
|
 |
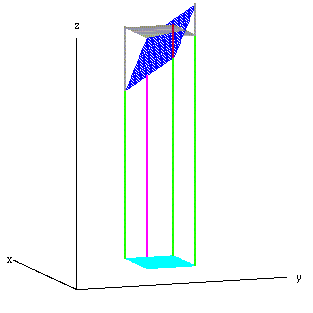
For visibility we turn the graph slightly, take out
the surface z = f(x,y)
and put in the horizontal plane z=f(a,b) in gray (at least
the piece above the light blue rectangle). It shows that
the vertices of the parallelogram adjacent to the point of tangency
are at distances fx(a,b)dx and
fy(a,b)dy below and above the horizontal plane
(both marked in gray) from that plane. So the fourth vertex
of the dark blue parallelogram is
df(a,b) = fx(a,b)dx +
fy(a,b)dy
from the horizontal plane (segment marked in dark red). It is the
change in z along the tangent plane as the corresponding
point in the xy-plane moves from (a,b) to
(a+dx,b+dy).
|
 |
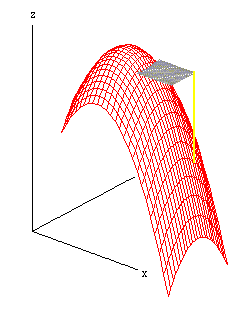
[Now the viewer is well above the xy-plane, but
behind the xz-plane, so that the point of tangency is visible.]
On the other hand, the yellow line shows the change
in z along the surface as the corresponding point in the
xy-plane moves from (a,b) to (a+dx,b+dy). Its
length is
f(a+dx,b+dy) - f(a,b) .
|
 |
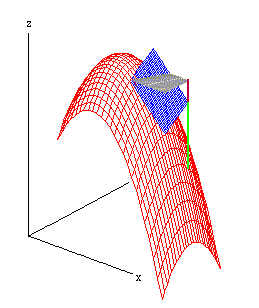
| Putting the dark blue part of the tangent plane
back in, we see that there is a substantial difference (in green)
between f(a+dx,b+dy) - f(a,b) (yellow in the last picture) and
df(a,b) (in dark red). The approximation is not good because
dx and dy are not small in this case. But the surface
is "locally linear": If we stay very close to any point in the
xy-plane, the corresponding piece of the surface would have
very little curve; it would be almost planar, so the approximation
of f(a+dx,b+dy) - f(a,b) by df(a,b) would be much better.
("Very close" changes
its meaning at different points on the surface: To make it seem almost
planar, one would have to cut out a much smaller piece
of the surface near the apex than further down the slope.)
|
 |



