The intersection of 2 surfaces

The Intersection of Two Surfaces

Though the theme of this page is the points that lie on both of two surfaces, let us begin with only one, the contour x²z - xy² = 4 or essentially z = (xy² + 4)/x². Let us suppose that we want to find all the points on this surface at which a vector normal to the surface is parallel to the yz-plane. It is not clear, at least to me, that there are any such points; as I picture vectors perpendicular to the surface, they all seem to go forward or backward, at least slightly. But let us see what calculus tells us.
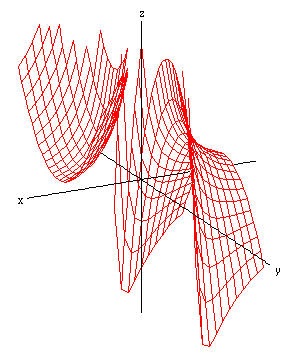
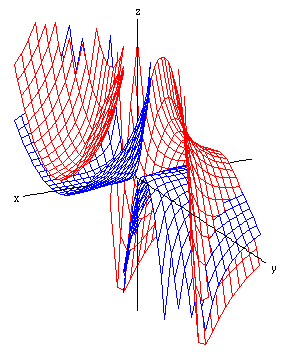
All vectors normal to the surface at a point (x,y,z) on it are multiples of the gradient (2xz-y²)i - 2xyj + x²k at that point, so to say that the normal is parallel to the yz-plane is to say that 2xz - y² = 0. So the desired points are on both the original surface and the new surface determined by this new equation (shown in blue to the right).
It appears from the diagram above that there are no points with positive x-values that are on both surfaces at the same time; but in the region where x < 0 and z < 0, it appears that the two surfaces intersect, i.e., they have some points in common. Those points are arranged in two curves, drawn in green in this diagram.

Algebraically, we are looking for the points (x,y,z) that make both of the equations true:

x²z - xy² = 4 2xz - y² = 0 In some cases this may the simplest way to describe algebraically a curve in space: as the set of common solutions of two or more equations. But in this case we can use another method, which may be more useful: giving the coordinates of the points on the curve by expressions in some common variable (called a "parameter") which may or may not be one of the coordinates. In this case we can express y and z,and of course x itself, in terms of x on each of the two green curves, so we can "parametrize" the intersection curves by x: From the second equation we get y² = 2xz, and substituting into the first equations gives x²z - x(2xz) = 4, or z = -4/x² -- from which we can see immediately that the z-values will be negative. From the equation y² = 2xz we can see that the x-values will also be negative; and substituting into this equation our expression for z in terms of x shows that y = ±sqrt(-8/x). So we have the desired parametrizations of the intersection curves:
x = x, y = ±sqrt(-8/x), z = -4/x²

Roughly, what we expect is that a single equation in three variables determines a surface in space; two equations determine a curve or curves (in the sense that the common solutions (x,y) of both equations form one or more curves); and three dermine a point or isolated points. Of course, exceptions abound: The solutions of the single equation x² + y² = 0 is the (one-dimensional) z-axis. And if we consider the infinitely many planes that all pass through the same line, then any two or more of their corresponding (linear) equations will still determine that common line. But "each new equation cuts down the dimension by one" is a handy rule of thumb.

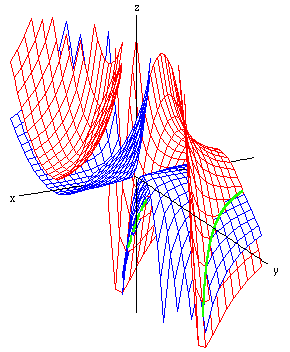
Because I mentioned above that it is hard to see whether any points on the original surface x²z - xy² = 4 have the property that the normals there are parallel to the yz-plane, let us take one of the points on our curve and look at the gradient vector there, to see whether it has the desired properties.

One point on the surface is (-2,2,-1), and the gradient there is 8j + 4k, so it is clearly parallel to the yz-plane. The real question is the more basic one: Is it true that the gradient is always perpendicular to the contour at its base? Here is a piece of the original surface, with (-2,2,-1) at one corner and with the above gradient vector drawn in dark green.

The reader is invited to download the corresponding Winplot file and rotate it to see that gradient is indeed perpendicular to the surface.