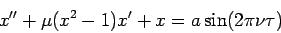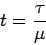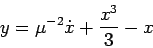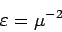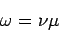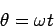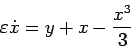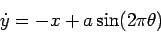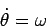Warren Weckesser
One form of the periodically forced
van der Pol equation is
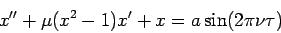We are interested in the case where μ is large.
By making the definitions
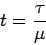
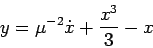
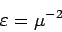
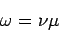and
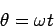
we can convert the second order differential equation
into the following autonomous three dimensional system:
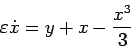
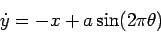
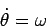
This is the system studied by me and my collaborators John Guckenheimer
and Kathleen Hoffman.
Our results are reported in publications 4, 6, 8, and 9 listed in
my CV.
The following plot shows an example of the phase space of this system.
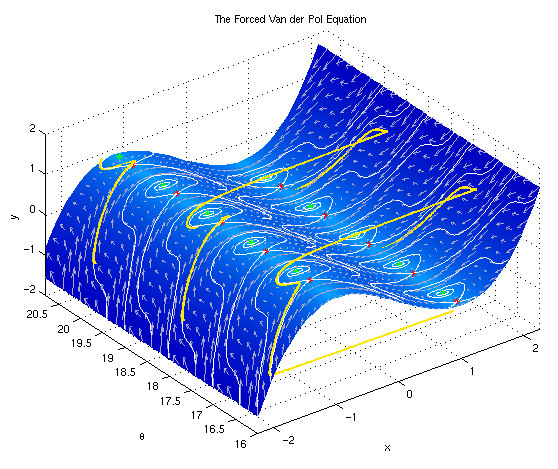The yellow curve is a solution to the system of equations when
ε is small but positive.
The blue surface is the critical manifold and the
white vector field shows the slow subsystem that results
when ε = 0.
The red and green markers are folded equilibria.
These are equilibria of the "desingularized" slow subsystem, but
they are not true equilibria of the original equations
when ε > 0. The red markers are folded saddles, and
the green markers are folded spiral points.
In publication 8 (see also 9), we studied a Poincare map
defined as in the following plot:
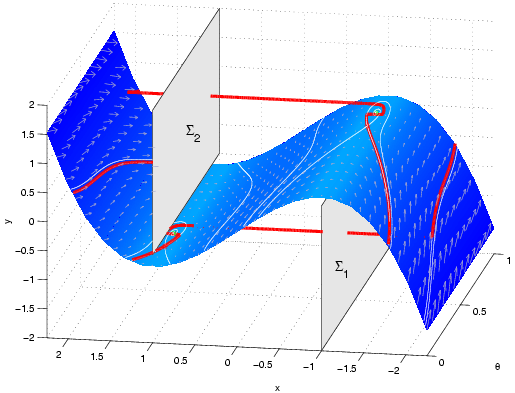We computed the map from Σ1 to Σ2
by solving the differential equations. The map was completed
by using a symmetry of the differential equations to map
Σ2 to Σ1.
The following plot shows a horseshoe map that occurs in
this Poincare map.
The images of the short segments at the top and bottom
of the red parallelogram are plotted in cyan.
(There are two cyan curves in the plot, but they
are very close together.)
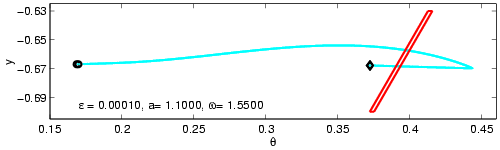This plot was computed using AUTO, by setting up
the computation of the Poincare map as a boundary value
problem, and by doing continuation in the initial conditions.
