Introduction to Related Rates Problems

(Problems adapted from Calculus by James Stewart, 1^st edition)

1. Express the volume of a cube as a function of the length of one side of the cube.
2. Express the area of a circle as a function of the radius of the circle.
3. Express the volume of a sphere as a function of the radius of the sphere.
4. A streetlight is at the top of a 15 ft pole. A man 6 ft tall walks away from the pole along a straight path. Express the length of the man's shadow as a function of the distance from the man to the pole.
5. A spotlight sits on the ground and shines on a wall that is 12 m away. A man 2 m tall is walking from the spotlight toward the building. Express the height of his shadow as a function of his distance from the building.
6. A plane flies horizontally at an altitude of 1 mi passes directly over a radar station and keeps flying. As the plane flies, the distance that the radar must travel to hit the plane is increasing. The horizontal distance, along the ground, from the station to the point on the ground below the plane is also increasing. Find an equation that relates the two distances.
7. A baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward first base. Find an equation that relates her distance from third base to her distance from home base. Also, find an equation that relates her distance from second base to her distance from home base.
8. Two cars start from the same point at the same time. One travels south at 60 mi/h, and the other travels west at 25 mi/h. Find an equation that relates the number of hours they have driven to the distance between the two cars.
9. At noon, Ship A is 150 km west of Ship B. Ship A is sailing east at 35km/h and Ship B is sailing north at 25km/h. Find an equation that relates the number of hours since noon to the distance between the two ships.
10. At noon, Ship A is 100 km west of Ship B. Ship A is sailing south at 35km/h and Ship B is sailing north at 25km/h. Find an equation that relates the number of hours since noon to the distance between the two ships.
11. A man starts walking north at 4 ft/s from a point P. Five minutes later a woman starts walking south at 5 ft/s from a point 500 ft due east of P. Find an equation that relates the number of minutes that the woman has been walking to the distance between them.
12. A boat is pulled toward a dock by a rope attached to the bow (front) of the boat and passing through a pulley on the dock that is 1 m higher than the bow of the boat. Find an equation that relates the length of the part of the rope between the boat and the pulley to the (horizontal) distance from the boat to the dock.
13. A tank containing water is in the shape of an inverted cone. So it looks like an ice cream cone. The tank has height 6 m and top diameter 4 m. Water is leaking out of the tank, and at the same time water is being pumped into the tank. The water level in the tank is rising. Find an equation that relates the volume of the water in the tank to the depth of the water in the tank.
14. A trough is 10 ft long, and its ends have the shape of the isosceles triangles that are 3 ft across at the top and have a height of 1 ft. Water is being poured into the trough. Find an equation that relates the volume of water in the tank to the depth of the water in the tank. (Think of a trough of water that horses drink out of.)
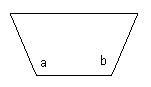
15. A water trough is 10 m long, and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm. The trough is being filled with water. Find an equation that relates the volume of water in the tank to the depth of the water in the tank. Here is an isosceles trapezoid: (The angles at a and b are supposed to be equal, and the top and bottom are parallel.)
    
16. A plane flies horizontally at an altitude of 1 km until it is above a ground radar station. Then the plane climbs at an angle of 30 degrees at 300 km/hr. Find an equation that relates the distance between the plane and the radar station to the time that the plane has been climbing.
17. Two people start walking from the same point at the same time. One walks east at 3 mi/hr and the other walks northeast at 2 mi/hr. Find an equation that relates the distance between the two people to the tune that they have been walking.
18. A ladder 10 ft long rests against a vertical wall. The bottom of the ladder slides away from the wall. (And the top of the ladder slides down the wall.) Find an equation that relates the angle between the wall and the top of the ladder to the distance between the bottom of the ladder and the wall.
19. A lighthouse is on a small island 3 km away from the nearest point P on a straight shoreline, and its light makes four revolutions per minute. Let L be the point that is the location of the lighthouse. Let B be the point at which the beam of light hits the shore. (Sometimes it points out to sea, of course, but we are not interested in that at the moment.) Find an equation that relates the angle PLB to the distance between P and B.