
1. If the position of a particle on a number line measured in feet is
at time t seconds, find the total distance traveled by the particle in the first 6 seconds, and diagram its motion.
2. What is the instantaneous rate of change of the volume of a spherical cell with respect to its radius (in cubic micrometers per micrometer --- a micrometer, denoted µm, is a millionth of a meter)? Explain why the result is the same as the surface area of the cell.
3. The cost of producing x widgets is
What is the instantaneous rate of change of total production cost with respect to number of widgets produced when x=200? (Economists call this the marginal cost of producing the 200th widget.)
4. (From Stewart, Single Variable Calculus, Early Transcendentals,
4th ed., Section 3.3, Exercise 19) Boyle's Law
states that when a sample of gas is compressed at a constant
temperature, the product of the pressure and the volume remains
constant: PV=C.
(a) Find the rate of change of volume with respect
to pressure.
(b) A sample of gas is in a container at low pressure
and is steadily compressed at constant temperature for 10 minutes.
Is the volume decreasing more rapidly at the beginning or the end
of the 10 minutes? Explain.
(c) Prove that the isothermal compressibility
[defined in the text as ß=(-1/V)(dV/dP)]
is given by ß=1/P.
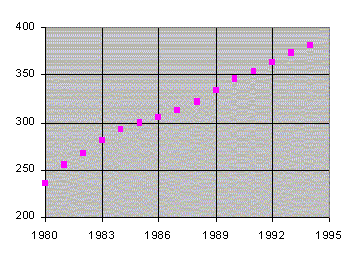
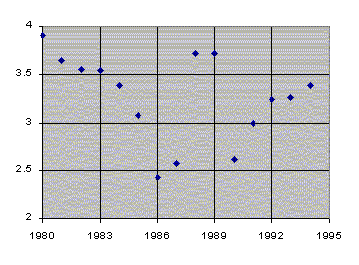
5. In the years 1980-94, the following table (source: The World Almanac and Book of Facts, 1995) gives the prices of wheat per bushel and the national weekly earnings of a production worker.
| Year | Wheat price | Week earnings |
|---|---|---|
| 1980 | 3.91 | 235.10 |
| 1981 | 3.65 | 255.20 |
| 1982 | 3.55 | 267.26 |
| 1983 | 3.54 | 280.70 |
| 1984 | 3.39 | 292.86 |
| 1985 | 3.08 | 299.09 |
| 1986 | 2.42 | 304.85 |
| 1987 | 2.57 | 312.50 |
| 1988 | 3.72 | 322.02 |
| 1989 | 3.72 | 334.24 |
| 1990 | 2.61 | 345.35 |
| 1991 | 3.00 | 353.98 |
| 1992 | 3.24 | 363.61 |
| 1993 | 3.26 | 373.64 |
| 1994 | 3.39 | 381.26 |
 |
The graph of weekly earnings against year is clearly linear, |
 |
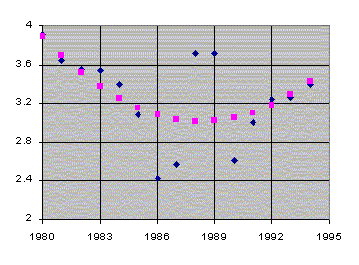
while the graph of weekly earnings against wheat prices reveals no pattern. |
 |
But the graph of wheat prices against years suggests a very roughly quadratic relationship. |
 |
Mathematical methods beyond the scope of the course can give us the quadratic equation that best fits the data ("best" in the sense that the sum of the squares of the "residuals", i.e., the vertical distances from the data points to the graph of the quadratic, is as small as possible). |
Using this quadratic approximation, we can approximate the rate of change of wheat price with respect to time, in dollars per year, at any fixed time, by drawing the tangent line to the quadratic.
| Year | Wheat price | Predicted | Residual |
|---|---|---|---|
| 1980 | 3.91 | 3.89 | 0.02 |
| 1981 | 3.65 | 3.69 | -0.04 |
| 1982 | 3.55 | 3.52 | 0.03 |
| 1983 | 3.54 | 3.37 | 0.17 |
| 1984 | 3.39 | 3.25 | 0.14 |
| 1985 | 3.08 | 3.15 | -0.07 |
| 1986 | 2.42 | 3.08 | -0.66 |
| 1987 | 2.57 | 3.03 | -0.46 |
| 1988 | 3.72 | 3.01 | 0.71 |
| 1989 | 3.72 | 3.02 | 0.70 |
| 1990 | 2.61 | 3.05 | -0.44 |
| 1991 | 3.00 | 3.10 | -0.10 |
| 1992 | 3.24 | 3.18 | 0.06 |
| 1993 | 3.26 | 3.29 | -0.03 |
| 1994 | 3.39 | 3.42 | -0.03 |