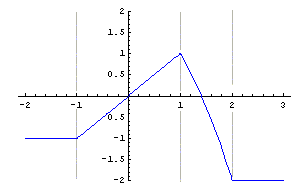
|
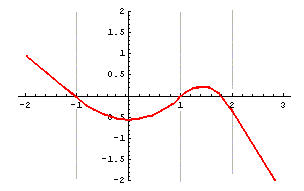
Thus, the graph of F
consists of pieces on each of the intervals on
which f is defined, as shown to the right.
But since we do not yet know the values of the constants
C1 to C4, we don't
yet know which piece is the correct one on each
interval -- choosing different values of a constant moves
the corresponding piece of the curve up and down.
We will have determined F when we
have found these constants.
|
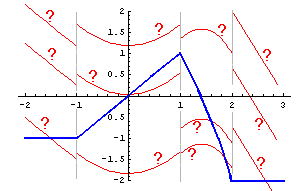 |
We first choose C2. Because F(x) is
defined as the integral of f from 1 to x, it
follows that F(1) is the integral of f from 1
to 1; so F(1) = 0 -- the integral of any function over
an interval of zero length is 0. Thus, we must choose
C2 so that the value of
.5x2 + C2 is 0 when
x=1. This forces
C2 = -.5(1)2
= -.5,
and we have determined one part of the antiderivative.
|
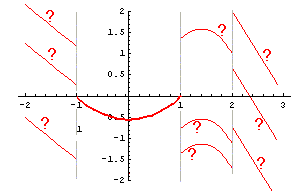 |
Next we use that fact that F is continuous (because it
has a derivative) to choose C3.
This constant is chosen so
that the limit of F as x approaches 1 from
above is 0 (i.e., F(1), as we noted while finding
C2), so:
2(1) - (1/3)(1)3 + C3
= 0
C3 = -5/3
|
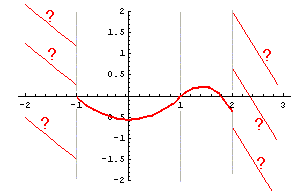 |
Similarly, we choose C1 so that the piece of
the graph for x-values less than -1 joins with the
piece of the graph for x-values between -1 and 1:
-(-1) + C1
= .5(-1)2 - .5
C1 = -1
And finally we choose C4 so that two
pieces match at x=2:
2(2) - (1/3)(2)3 - (5/3)
= -2(2) + C4
C4 = 11/3
|
 |
|
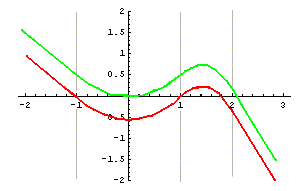
Finally, we note that this F is only one of the
antiderivatives of f, namely the one whose value
at x = 1 is 0. If we add any constant to F
throughout, we get a different antiderivative of f.
The graph in green shows the result of adding .5 to F,
resulting in an antiderivative of f that has value
0 at x = 0.
|
 |