AUTO

AUTO (or AUTO2000) is a software package for numerical continuation. The AUTO web page at Concordia University is http://indy.cs.concordia.ca/auto/, and the SourceForge web page for AUTO is http://sourceforge.net/projects/auto2000/.

The VFGEN AUTO Command

A C file that can be used by AUTO is created by the command

$ vfgen auto vector_field_file.vf

The name of the C file will be [name]_avf.c, where [name] is the name of the vector field given in the vector field file. Only the AUTO function called "func" will be complete. A "stpnt" function will created to serve as a template. The DefaultInitialConditions of the variables will be used for the values in the "stpnt" function; the file must be edited by hand to define an actual known solution. The remaining functions will be stubs that do nothing but return 0.

Any user functions defined in the vector field file are ignored in AUTO command.

Example 1

We consider this variation of the van der Pol equation:

εx'= y+x-x3/3
 y'= a-x
The vector field file is vanderpola.vf. The default value of ε specified in the file is ε=10-2.

The file created by

$ vfgen auto vanderpola.vf
is vanderpola_avf.c. A "constants" file (created by hand) is c.vanderpola_avf.

The AUTO script vanderpola.auto first does continuation in a of the equilibrium that is (0,0) when a = 0. (We don't really need to use AUTO for this, since the formula for the equilibrium is simply x = a, y = -a+a3/3.) There is a Hopf bifurcation when a = 1; the script computes the family of periodic orbits that arises from the Hopf point.

Here is a plot of the some of the periodic orbits computed by AUTO.

Family of periodic orbits
(This plot was created by the Python script vanderpola_plotpos.auto.) Those familiar with the van der Pol equation will recognize this family as the canards that separate the case of an attracting fixed point when a > 1 and the large amplitude relaxation oscillation that exists when -1+δ < a < 1-δ, where δ > 0 is a small number that depends on ε.

Example 2

In this example we first use VFGEN to convert the Mackey-Glass delay equation into a system of ordinary differential equations, and then use AUTO to find some of the bifurcations of the system. (See the DDE23 command or the DDE_SOLVER command for examples in which the Mackey-Glass equation is solved with a differential delay equation solver.)

We use the version of the Mackey-Glass equations defined in this file: mg.vf. The DefaultInitialCondition and DefaultHistory of the state variable x are both set to 1, because in the AUTO command, the DefaultInitialCondition is used for the default values of the STPNT function, and in the Mackey-Glass equation, x=1 is an equilibrium solution.

First, we use VFGEN to approximate the delay equation as a system of ordinary differential equations:

$ vfgen delay2ode:N=20,p=2 mg.vf > mg_2ode.vf
This creates mg_2ode.vf, which defines a 41 dimensional system of ODEs.

Next, we use VFGEN to create an AUTO C file for this system:

$ vfgen auto mg_2ode.vf
This creates the file mg_2ode_avf.c

We also need an AUTO constants file: c.mg_2ode_avf. (This was created by hand.)

Finally, we use an AUTO script to compute several bifurcation curves, in which the bifurcation parameter is the delay τ: mg.auto We run AUTO as follows:

$ auto mg.auto

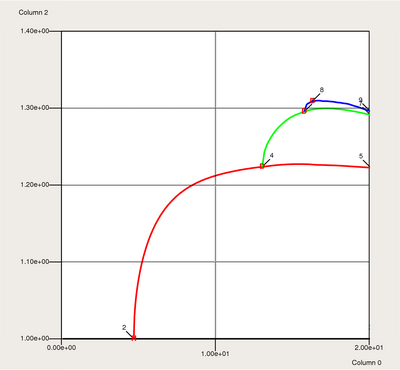
AUTO finds a Hopf bifurcation near τ=4.703, and a sequence of period doubling bifurcations at τ=13.05, τ=15.78, and τ=16.31. Presumably, this is the beginning of a period doubling cascade to chaos.

Here is the bifurcation diagram created by AUTO.

The horizontal axis is τ, and the vertical axis is the maximum x value of the periodic orbit. (Click on the image to see a larger version.)