Taylor Method

The idea of the Taylor method for approximating the solution to a system of differential equations is to expand the solution to
X'(t) = F(X)
in a Taylor series:
X(t+h) = X(t) + hX'(t) + (h2/2)X''(t) + (h3/6)X(3)(t) + ...
The differential equation gives us X'(t). To find X''(t), we differentiate the differential equation with respect to t (t arguments are suppressed):
X'' = DF(X)[X']
(We denote the r-linear differential DrF(X) acting on the vectors V1,...,Vr as DrF(X)[V1,...,Vr].) Differentiate again to find X(3) and higher derivatives of X:
X(3) = D2F(X)[X',X']+DF(X)[X'']
X(4) = D3F(X)[X',X',X'] + 3D2F(X)[X'',X'] + DF(X)[X(3)]
X(5) = D4F(X)[X',X',X',X'] + 6 D3F(X)[X'',X',X'] + 3D2F(X)[X'',X''] + 4D2F(X)[X(3),X'] + DF(X)[X(4)]
and so on.

The VFGEN Taylor Command

The taylor command of VFGEN creates a function that computes the Taylor expansion of X(t+h) to a given order. The order is specified with the order option. The general form of the command is

$ vfgen taylor:order=r vector_field_file.vf

The files created are [name]_taylor[r].c and [name]_taylor[r].h, where [name] is the name of the vector field given in the vector field file, and [r] is the order given with the order option. The C file [name]_taylor[r].c will contain the functions [name]_vf and [name]_taylor[r]. The first computes the vector field, and the second computes the Taylor approximation. Also defined in the C file are the functions [name]_diff[k], for k=1, 2, ..., r-1. These functions compute the k-linear differentials DkF(X)[V1,...,Vk]. These could be useful in programs that analyze bifurcations or that compute invariant manifolds.

(Were you looking for a command related to the program Taylor, by Maorong Zou and Àngel Jorba? A command for this program will be added to a future version of VFGEN.)

Options

order This option specifies the highest order retained in the Taylor series. The order must be a positive integer.
Default: order=5

Bugs and Limitations

Example 1

Here is a sample vector field file: pendulum.vf.
The file created by
$ vfgen taylor:order=7 pendulum.vf

are A short C program that uses these files is pend_main.c. A Makefile for the pend_main program is Makefile_pend_main. The program pend_main uses the function pendulum_taylor7 to implement a simple solver for the differential equations. Here is a plot of the output of pendmain:
The following plot shows a comparison of the polynomial approximations for orders 3, 7, and 15 for the pendulum vector field. The Taylor expansion was found for θ(0)=3.0 and v(0)=0.1, with parameter values g=9.81, b=0.25, L=1, and m=1. (For example, the data for the order=3 case was created with pend_taylor_demo3.c.) Also shown is the solution generated with the GSL ODE solver (with abserr=10-12 and relerr=10-10).

Example 2

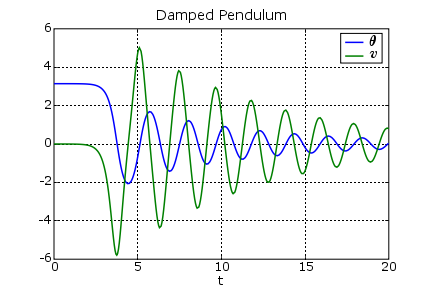
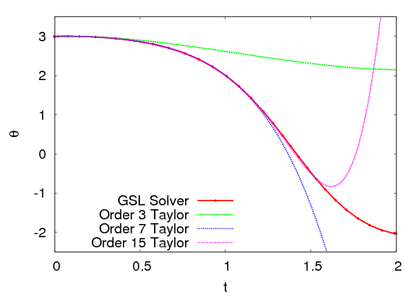
A vector field file for the van der Pol equation is vanderpol.vf. The file vanderpol_adaptive8.c implements an adaptive solver that uses an order 8 Taylor method to solve the differential equation. The code works by using the Taylor polynomial at x(t) to estimate x(t+h). Then, the Taylor polynomial at x(t+h) is used to compute the value at x(t). If this value differs from the original x(t) by more than tol, the step size is reduced by 2/3, and the test is tried again. If the difference is less than tol, the solution is advanced. If, in addition, the solution is less then mintol, the step size is increased by a factor of 1.5.

(This method was implemented as a fairly simple test of the code generated by VFGEN. There are smarter ways to adapt the step size--see, for example, the documentation of the Taylor program by Zou and Jorba mentioned above.)

The program uses the functions defined in the C files created by the command

$ vfgen taylor:order=8 vanderpol.vf
A Makefile for the solver is Makefile-vanderpol_adaptive8; the solver is compiled and run as follows: 
$ make -f Makefile-vanderpol_adaptive8
$ ./vanderpol_adaptive8 > vdp8.dat
The parameter values used in the file vanderpol_adaptive8.c are: ε=10-3, tol=10-8, mintol=10-10.

For comparison, a solver that uses the GNU Scientific library is created (also with VFGEN): 

$ vfgen gsl:demo=yes vanderpol.vf
$ make -f Makefile-vanderpol
$ ./vanderpol_solve epsilon=0.001 relerr=1e-7 abserr=1e-9 > vdpgsl.dat
A solver that uses RADAU5 is created with 
$ vfgen radau5:demo=yes vanderpol.vf
and then the driver program vanderpol_dr5.f is modified to use ε = 0.001, and the relative and absolute tolerances are set to 10-7 and 10-9, respectively. The RADAU5 driver is compiled as shown in the RADAU5 section of the web page.

Solutions generated by the GSL solver and by the adaptive Taylor solver are shown in the following plot. Only the interval 8.5 < t < 10 is shown.

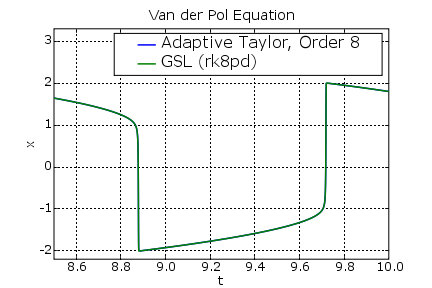
The plots are indistinguishable. The adaptive Taylor method generates 4767 data points, the GSL solver generates 4904, and the RADAU5 solver generates just 1191 points. The final values (at t=10) of the x and y coordinates of the numerical solutions are
Adaptive Taylor (Order 8) 1.80308347 0.150123424
GSL 1.80308347 0.150123395
RADAU5 1.80308348 0.150123481

Example 3

The vector field file MorrisLecar.vf defines the Morris-Lecar system of equations. The vector field formulas involve cosh and tanh, so the lengths of the expressions for the derivatives grow quickly as the order increases. Here, for example, are the files generated with order=15: The longest line in MorrisLecar_taylor15.c is over 10,000 characters. (Nevertheless, the GNU GCC compiler is able to compile this file.)