VFGEN § DDE23

DDE23

The DDE23 function in MATLAB solves differential delay equations with constant lags.

The VFGEN DDE23 Command

A set of MATLAB files configured to use the DDE23 function are created by the command

$ vfgen dde23 vector_field_file.vf

The vector field must have at least one delay expression, and the delay can not depend on the independent variable or on any state variables.

Options

parstyle

The method by which parameters are passed to the MATLAB functions generated by VFGEN is controlled by the parstyle option. The default is parstyle=vector, and the alternative parameter style is specifed with the option parstyle=list. When parstyle=list is given as

$ vfgen dde23:parstyle=list vector_field_file.vf

each parameter is listed explicitly as an argument of MATLAB functions. That is, instead of

[name]_dde23(t,x,Zlags,p)

the vector field function will be

[name]_dde23(t,x,Zlags,param1,param2,...,paramM)

Default: parstyle=vector

demo

If the option demo=yes is given, the file [name]_dde23_demo.m is created. This MATLAB file defines the function

function [name]_dde23_demo(stoptime)

which when called will solve the equations using DDE23 (with the default initial conditions and parameters) for the time interval 0 ≤ t ≤ stoptime.
Default: demo=no

Example 1

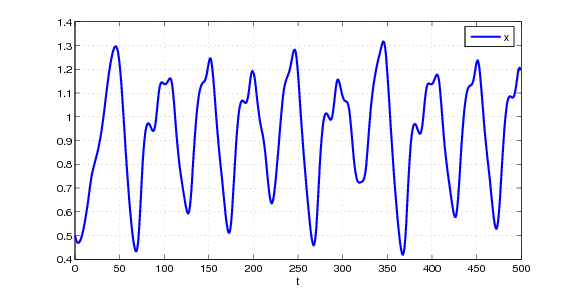
The Mackey-Glass equation is

x'(t) = -b*x + a*x(t-τ)/(1+x(t-τ)¹⁰)

Here is the Mackey-Glass vector field file: MackeyGlass.vf.
The files created by

$ vfgen dde23:demo=yes MackeyGlass.vf

are

Here is the plot generated by the MATLAB command MackeyGlass_dde23_demo(500):

Example 2

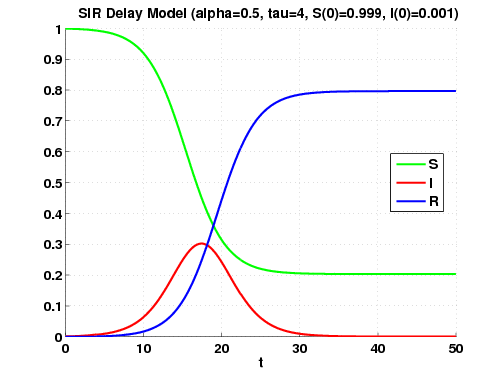
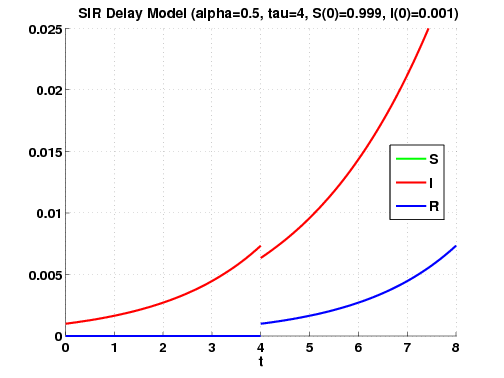
The SIR delay equations are

S'(t)	=	-α S I
I'(t)	=	α (S I - S(t-τ) I(t-τ))
R'(t)	=	α S(t-τ) I(t-τ)

These equations are a simple model of the spread of a disease in a well-mixed population in which each individual is infectious for exactly τ time units.

The file SIRdelay.vf is a vector field file for this system.

We create a MATLAB function that may be used with the DDE23 library with the command

$ vfgen dde23 SIRdelay.vf

The file created by this command is SIRdelay_dde23.m.

The file SIRdelay_dde23_solver.m was written to use the DDE23 function generated by VFGEN to solve these equations.

Here is the plot generated by the command SIRdelay_dde23_solver(50):

Here is a detail of the above plot. The discontinuity at t = 4 (when the initial cohort of infectives all recover simultaneously) was handled explicitly in the MATLAB code.